Fractals in Rust
Rust and Python have a common problem: they both make it really easy to do very complex things in a single step. As a result, this video about rendering the Julia set sent me down a fractal hole.
Fractals aren’t something I’ve played with much before, so first I needed to go look at some math. Quadratic Julia sets, it turns out, are fairly simple. They’re generated using the mapping $f(z) = z^2 + c$ for a fixed $c$ and almost all values of $c$ will generate something. Notable exceptions to this are -2 and 01.
To create a Julia set fractal $z$ is initialised using the coordinates for each pixel within the image space and then repeatedly updated, calculating its magnitude on each iteration. The result of this calculation is used to identify whether or not to colour the pixel.
So the key steps are:
Complex number multiplication
Alright, it’s been a while lets look at multiplying complex numbers… like binomials complex numbers are multiplied using the FOIL method (Firsts, Outers, Inners, Lasts). Which gives me
\[(a+bi)(c+di) = ac + adi + bci + bdi^2\]However, because $i^2$ is always -1 this can be simplified to2
\[(a+bi)(c+di) = (ac-bd)+(adi+bci)\]That’s not super complicated to to replicate, especially if tuples are used to represent the numbers:
fn complex_multiplication(n1: (f64, f64), n2: (f64, f64)) -> (f64, f64) {
let re = (n1.0 * n2.0) - (n1.1 * n2.1);
let im = (n1.0 * n2.1) + (n1.1 * n2.0);
(re, im)
}
And can be extended to return $z^2 + c$:
fn step(z: (f64, f64), c: (f64, f64)) -> (f64, f64) {
let re = (z.0 * z.0) - (z.1 * z.1) + c.0;
let im = (z.0 * z.1) + (z.1 * z.0) + c.1;
(re, im)
}
Magnitude
Having updated the value of $z$ you need to check whether its magnitude has gone above 2 (thus taking it outside the edge of the set), the greater the number of iterations required to do this the brighter the pixel will be. As a complex number can, for these purposes, be considered coordinates; the magnitude is equivalent to the hypotenuse of the right angle triangle formed by the x-axis and an imaginary perpendicular line intersecting the point itself.
let hypotenuse = (re * re + im * im).sqrt();
Is it in the Julia set?
Sticking with greyscale as used in Tim’s video that gives:
fn step(z: (f64, f64), c: (f64, f64)) -> (f64, f64) {
let re = (z.0 * z.0) - (z.1 * z.1) + c.0;
let im = (z.0 * z.1) + (z.1 * z.0) + c.1;
(re, im)
}
fn julia(c: (f64, f64), x: f64, y: f64) -> u8 {
let mut re = x;
let mut im = y;
for i in 0..255 {
let hypotenuse = (re * re + im * im).sqrt();
if hypotenuse > 2.0 {
return i as u8;
}
(re, im) = step((re, im), c)
}
255
}
Which is almost twice as long as the original but doesn’t require any imports.
Generating the image
This bit of code is essentially the same as it was in Tim’s video with a couple of minor changes:
- I increased the image size
- I switched from using 3.0 as the scaling factor to using $Pi$ which should improve the centering - though plausibly not noticeably. Regardless, I have no desire to create a Mail Sorting Engine so we’ll stick with observed constants rather than coerced ones3.
fn main() {
let width = 1920;
let height = 1080;
let scale_x = PI / width as f64;
let scale_y = PI / height as f64;
let mut img = ImageBuffer::new(width, height);
for (x, y, pixel) in img.enumerate_pixels_mut() {
let cx = x as f64 * scale_x - PI/2.0;
let cy = y as f64 * scale_y - PI/2.0;
let c = (-0.8, 0.156);
let value = julia(c, cx, cy);
*pixel = Rgb([value, value, value])
}
let _ = img.save("julia1.png");
}


Adding colour
Assigning the same number to each colour channel gives a greyscale image. To get a coloured image we need to mutate the distance value to make the values slightly different in each channel. After reading through KrazyDad’s extremely comprehensive tutorial4 I settled on this range of colours:
To build RGB values from the single return value we need to convert each value using the following attributes:
- frequency: how close to make the sine wave oscillations (period)
- width: the maximum value we can get out (amplitude) - this wants to be approximately half our total range so, as the maximum valid number is 255 this should be 255/2 or ~128
- center: the center position of the wave (where the zero point is)
- phase: how far to offset the wave from 0
Rust doesn’t have Python style list comprehensions natively (they can be added with cute) but it does provide an
enumerate function so this rather repetetive assignment
can be done in a DRY manner.
const COLOUR_FREQUENCY: f32 = 0.3;
const COLOUR_WIDTH: f32 = 140.0;
const COLOUR_CENTER: f32 = 50.0;
fn main() {
// snip
for (x, y, pixel) in img.enumerate_pixels_mut() {
// snip
let mut rgb = [0; 3];
for (idx, phase) in [3.0, -1.0, 1.0].iter().enumerate() {
rgb[idx] = (f32::sin(COLOUR_FREQUENCY * value + phase) * COLOUR_WIDTH + COLOUR_CENTER) as u8;
}
*pixel = Rgb(rgb);
}
}
On its own this works but it’s a touch stark as each value is discrete. Increasing the iterations and subtracting a fractional amount ($\log_2(\log_2(|z|))$) from the return value gives smoother contours. Be warned though, if you end up with an amorphous blob this takes AGES to generate due to the sheer number of pixels inside the shape.
for i in 0..5000 {
let hypotenuse = (re * re + im * im).sqrt();
if hypotenuse > 2.0 {
return i as f32 - (hypotenuse.log2()).log2() as f32;
}
(re, im) = step((re, im), c)
}
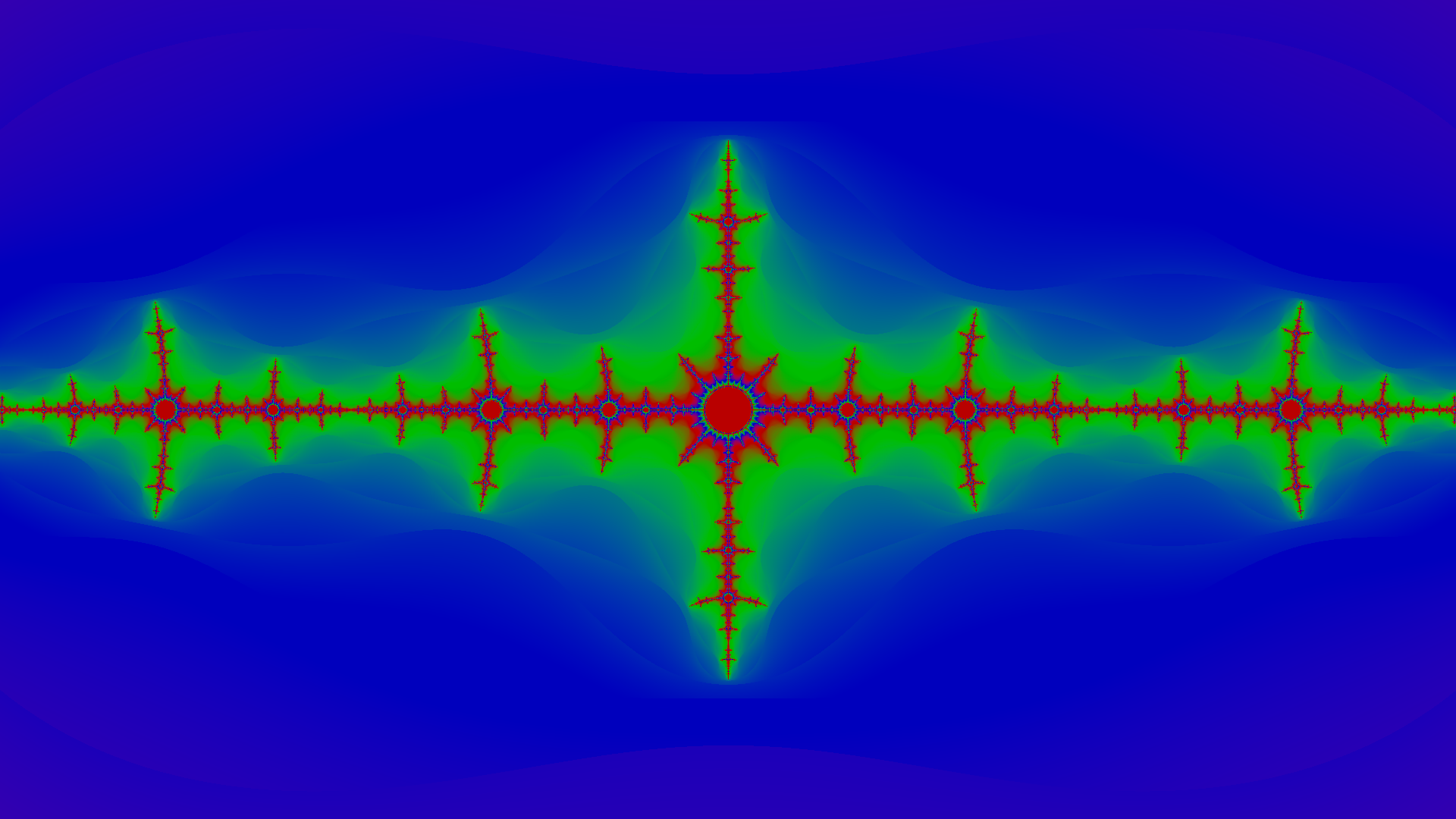
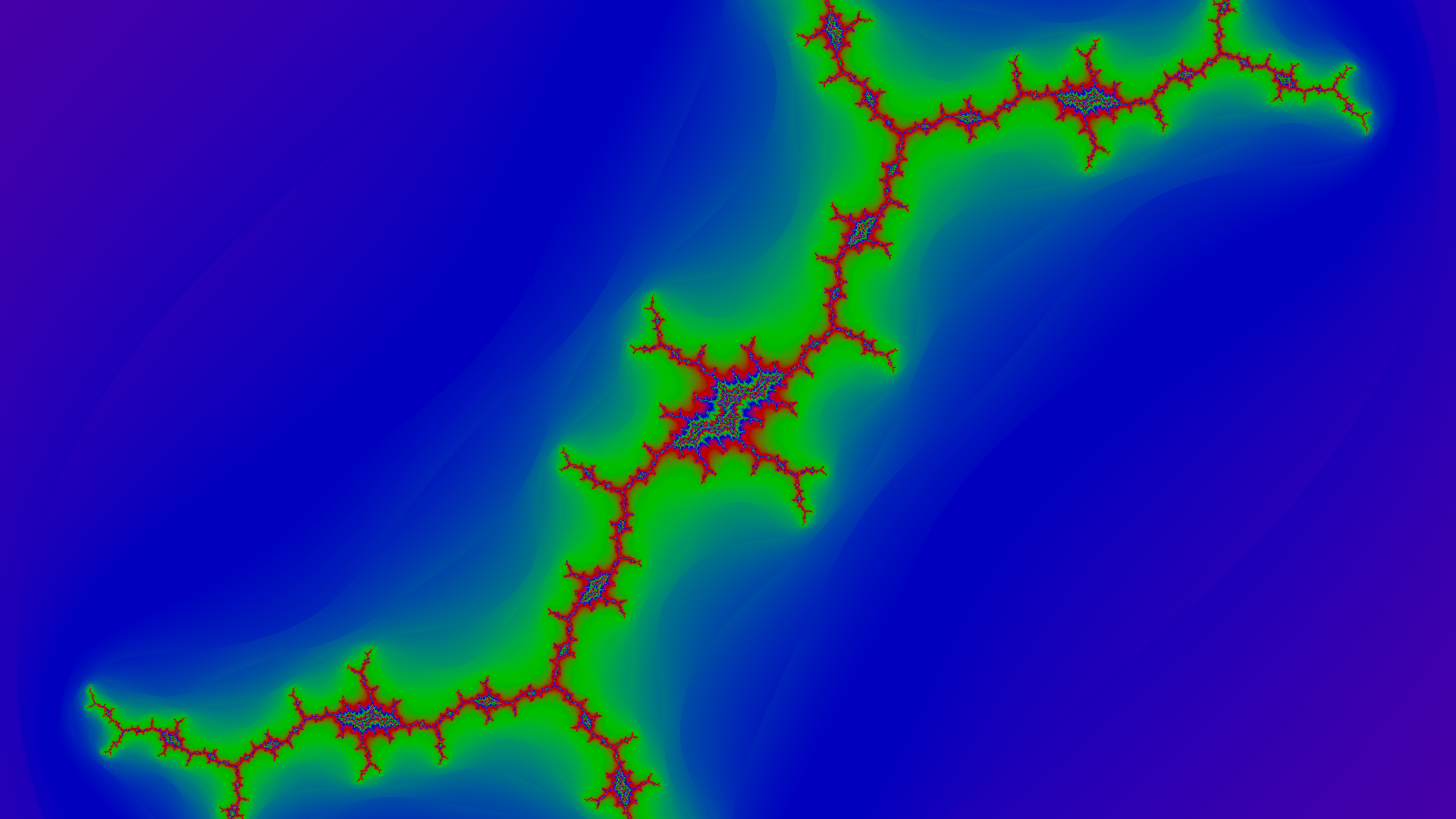

Comparison
To see how far we’ve come from the original output of the code, here it is side by side with the same fractal ($c = -0.8+0.156i$) generated using the updated code.

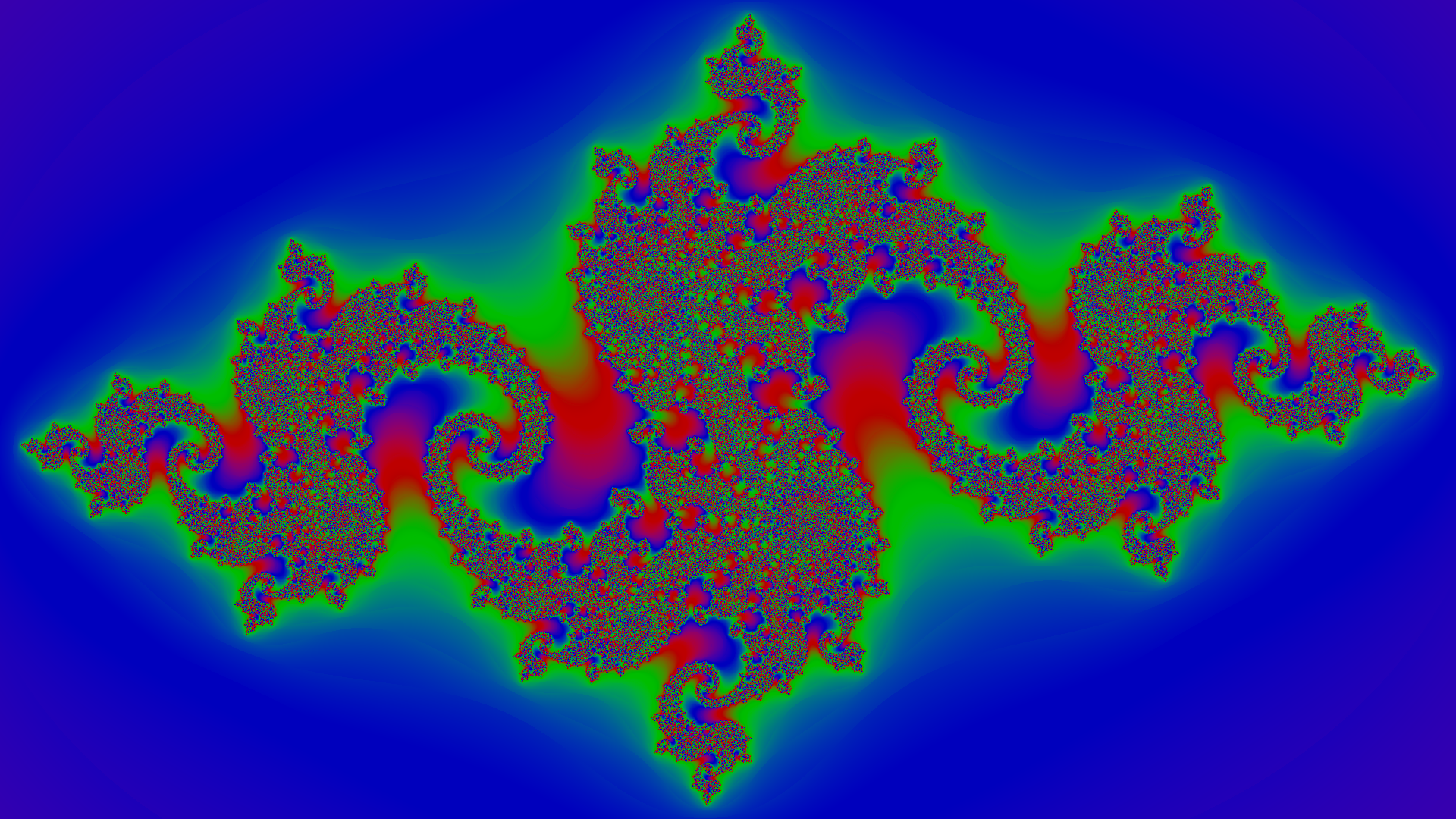
Resources
- Understanding Julia and Mandelbrot Sets
- Fractals continuous colouring
- Optimising a Julia Fractal Animation
-
For an actual explanation see Maths is Fun: Complex Number Multiplication. ↩
-
Pratchett, Terry. Going Postal. 2005. Corgi. (Support your local independent booksellers.) ↩
Comments powered by Talkyard.